Some Aspects of the Use of Americium as a Nuclear Fuel

[NNadir]

Last edited Sun Mar 23, 2025, 11:48 AM - Edit history (1)

The paper to which I'll refer is this post is this one: Janne Wallenium Physics of Americium Transmutation Nuclear Engineering and Technology 44, 2, 2012, 199-206

Since I have no formal training in nuclear engineering, an area in which I am completely autodidactic, I am untroubled by being prevented from having "crazy" ideas. To be perfectly honest, over some decades, I have been disabused of many these ideas by educating myself as to why they are crazy, which of course, is a process of learning new things, which should be the goal of any autodidact in any field, whether it nuclear engineering or proteomic implications in neurophysiology, or even the study of history of ballet. Nevertheless, what is fun and somewhat useful for me in nuclear engineering is to struggle backwards against understanding the craziness of the original ideas to see if I can find a way to make them less crazy.

In recent years, I have been very interested in the properties of metallic nuclear fuels, in particular, the transuranic metals, neptunium, plutonium (where I am fascinated by the allotropes and the liquid) and most recently americium and curium.

Since my son's girlfriend, who is formally trained in nuclear engineering, as is my son, declared to me when I first met her that her favorite element was americium, this has led me to return to some previous thinking about this element and expand upon my thoughts around it. The element is considered a problematic component of so called "nuclear waste," which is a term used in common parlance – a parlance I find regard as rote and foolish – for valuable used nuclear fuel. Many people have mused on ways to "transmute" americium into curium, in particular, one or both of two isomers ²⁴²Cm with t_1/2 = 163 days, and ²⁴⁴Cm t_1/2 = 18.11 years, as opposed to the half-lives of the precursors ²⁴¹Am, t_1/2 = 432.6 years, and ²⁴³Am, t_1/2 = 7370 years. The upside of this procedure would be the recovery of significant energy from these valuable isotopes of americium via nuclear decay of the curium isotopes via alpha emission. Of course, if an isotope of americium fissions, it is also transmuted into fission products, other elements distributed around the center of the periodic table, nearly all of which, in my opinion anyway, are valuable products in their own right. (Over the years I've thought of many interesting applications for technetium, which can only be obtained from used nuclear fuels.)

Transmutation into curium is certainly feasible, but from my perspective, a more interesting way to use americium would be via fission, during which some, but not all, of the americium isotopes would be transmuted into the aforementioned curium isotopes. Yet, to repeat, there would also be valuable fission products worthy of recovery and use.

Actually, the paper above, while its title refers to transmutation, certainly includes some very interesting commentaries on fission.

I have been contemplating this for some times, and my latest americium reactor design, which may or may not be "crazy," involves a biphasic coolant that will itself be radioactive, resulting in the useful transmutation and decay of fission products, this with a heat transfer component. The details are unimportant but are dependent on an interesting property of the three accessible americium isotopes, which is that upon fission, they apparently have a feature, at least are believed to have a feature, of producing more neutrons per fission than many other fissionable actinides: This is called "multiplicity" an important factor in nuclear engineering. It is most often designated by the Greek letter "eta" which is not accessible from the DU editor. (See below). This means that they can recover some or all of the neutrons that went into making them, three for ²⁴¹Am (from ²³⁸U) and five for ²⁴³Am from the same source, particularly if one includes spontaneous fission neutrons.

Some time ago in this space, I reported on the calculated critical masses of americium isotopes: Critical Masses of the Three Accessible Americium Isotopes.

Anyway, as I "fact checked" my potentially "crazy" reactor design, I was reminded of some important concepts in nuclear engineering that are important and differ significantly from other fuels, and thus require some consideration to prevent thermal runaway reactions resulting from transient supercriticality.

From the paper's introduction:

Introduction

Separation and transmutation of americium and curium, in addition to plutonium, would permit a reduction of high level waste inventories by more than a factor of 100. The time needed to store the residual waste would consequently shrink dramatically and the capacity of geological repositories would increase significantly. Conducting the recycle of americium and curium in light water reactors would however lead to a very high inventory of neutron emitting ²⁵²Cf in fuel cycle facilities, requiring expensive investments in shielding. Hence, these elements should be directed to fast spectrum systems, which would reduce the inventory of ²⁵²Cf by more than a factor of 100 [1]. The safety problems appearing when introducing minor actinides into the fuel are however still prevalent in a fast neutron spectrum, and in certain cases they are even more problematic than in a light water reactor. Compared to a “standard” breeder reactor with (U, Pu)O2 fuel, the presence of americium will lead to:

1. A reduction in Doppler feedback
2. An increase in coolant temperature coefficient
3. A smaller effective delayed neutron fraction.

This noted, let me offer my personal opinion on a popular and sometimes actually practiced (for example in Scandinavian countries) idea about so called "nuclear waste," which is the use of "geological repositories" for disposing the components of used nuclear fuel. To me, this is a very bad idea, not quite as bad as, say, carbon dioxide sequestration, but not a good idea either. The concept of there being something called "waste" is, at the risk of stating a truism, wasteful. When I think about nuclear designs, I am always thinking about using the components of used nuclear fuels, either internally or externally from the reactor itself, in fact, beyond Americium, or plutonium, or neptunium and uranium.

Doppler feedback us a function that in atomic nuclei neutron absorbances, both those that capture neutrons, which add an atomic mass unit to the nuclei, potentially inducing radioactivity or converting a radioactive nucleus into one that is stable, are subject to what are called "resonances."

Here for example is the "capture cross section" of a fission product, an isotope of cesium, ¹³⁵Cs, that is radioactive and has a long half-life, t_1/2 = 3,200,000 years.



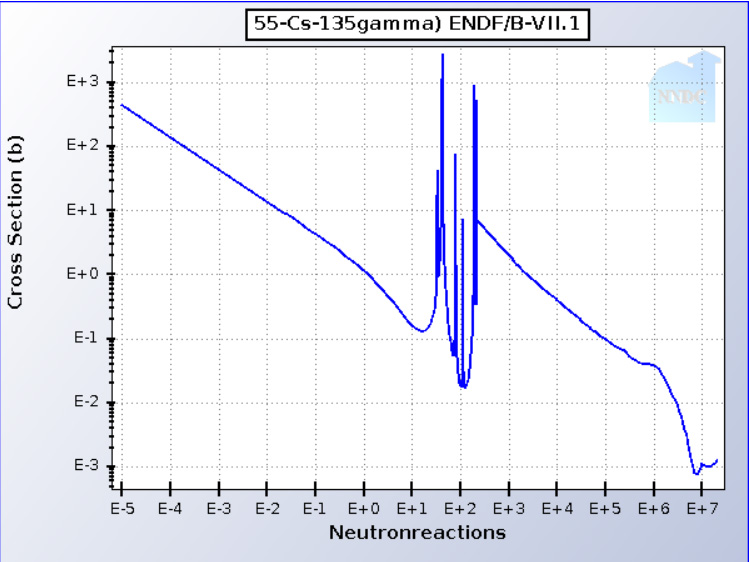
In this diagram the "cross section" has units whimsically named (during the Manhattan project) as "barns," a unit of area equal to 10^-28 m², which is the apparent "diameter" of the atomic nucleus as it "appears" to an approaching neutron. As this is in the quantum realm, the "diameter" changes depending on the speed of a neutron.

The x-axis denotes the kinetic energy of neutrons in electron Volts (eV), the y-axis represents the probability that ¹³⁵Cs will absorb a neutron and be converted into another isotope of cesium, ¹³⁶Cs, which is also radioactive but has a much shorter half-life than the isotope from which it formed. ¹³⁶Cs, t_1/2 = 13.16 days, decaying into nonradioactive ¹³⁶Ba, an isotope of barium. (Note that this is a log-log plot.) In a typical thermal reactor, in which the neutrons are moderated, i.e. slowed down to the average speed of molecules or atoms at a given temperature (as described in statistical mechanics). For most thermal reactors, the type of reactor that dominates the world nuclear fleet, the kinetic energy of slow neutrons is taken to be 0.253 eV. In a "fast" reactor, by contrast, the neutrons will have energies close to the energy they have when released during fission, typically on the order of 1-2 MeV, 1-2 million electron-volts, "E6" on the graph. The region between E6 and E-1 (thermal) neutrons is referred sometimes as the "epithermal region."

Note that the graph is not smooth; there are several sharp peaks between 50 eV and 250 eV where the probability of absorbing a neutron, again, known as its "cross section" (which, again, has units of area) becomes dramatically higher, albeit at narrow regions of neutron energy. Actually nuclei can have several "cross sections," one for absorbance, as shown above, one for scattering, the probability that a neutron will strike a nuclei without being absorbed but rather giving up some of its kinetic energy (slowing down) and for heavy nuclei (and indeed, more rarely, some light nuclei) will fission, that is split. These cross sections do not depend intimately upon one another. They are not really size related in a classical sense, but are actually features of the often less than intuitive quantum world. No matter. To the extent that they behave classically, they are subject to the Doppler effect, an atom moving in the same direction as a neutron that strikes it will have an apparently lower energy for absorbance on the x-axis, than one that is not moving much, whereas an atom moving toward an approaching neutron will have an apparently higher energy at which the absorbance occurs. This, the Doppler effect, most familiar in the science of stars, and also in the sound of cars and locomotives as they approach or recede with changing pitch.

Heat, temperature, as we know, is actually a function of molecular motion. Irrespective of the phase, solid, liquid or gas, in or out of molecules, atoms are always in motion, and the hotter they are, the faster they are moving, or in solids vibrating until the vibrations become so strong as to induce melting. In follows that Doppler effects are stronger at higher temperatures. Since the motions are more or less random in combinations of three directions, the tendency of the Doppler effect is to broaden the resonances, to smooth them out since they are wider.

Heavy nuclei can either fission or absorb. The former generally increases the population of neutrons; the latter decreases the population of neutrons. The ratio between the probability of capturing a neutron, and being transmuted to another isotope one atomic mass unit (amu) higher than the original nucleus, and the probability of undergoing fission instead, unspectacularly called the "capture to fission ratio" is an important parameter in understanding nuclear fuels and thus the engineering of nuclear reactors which must be capable of converting heat into exergy, i.e. useful energy, while maintaining structural and operational integrity. In general, the value of this ratio varies with the energy of the neutrons striking the nuclei, as was the case for absorption of a neutron (capture) by ¹³⁵Cs shown in the graphic above.

The theory of neutronics, builds on the classical theory of the statistical mechanics of gases, outlined in the 19th and early 20th centuries by Maxwell and Boltzmann, which resulted in the famous formula known as the Maxwell-Boltzmann distribution. It’s been many years since I last looked through the “Los Alamos Primer” written by Robert Serber to orient scientists joining the Manhattan project, where of course, much of the first developments in nuclear reactor and of course, the physics of nuclear weapons. Part of the Primer as I recall, referred to this distribution, but with the caveat that neutrons can pass through many materials instead of being reflected, and further can interact with other molecules so as to be consumed, and in fission, generated.

An aspect of the equipartition of energy in statistical mechanics, with which the Maxwell-Boltzmann distribution is involved, allows for the development of a concept of “neutron temperature.” Most neutrons released from a nucleus undergoing fission emerge at energies of approximately 1-2 MeV (millions of electron-Volts). A 2 MeV neutron has a speed that is about 6.5% the speed of light (where, rigorously, relativistic effects must be considered, but I’ll skip that refinement – of neutron mass - for the purposes of approximation). The “temperature” of such a neutron is roughly equivalent to the average speed of atoms (ions actually) at 15 billion degrees Kelvin. Despite these speeds, neutrons do not travel very far, they rapidly collide, many times in miniscule fractions of seconds, with atoms and molecules in the fuel and coolant, initially at high speeds, where they are mostly scattered, surrendering some their energy, thus “cooling” the neutron while redistributing some its energy to the atoms with which they collide thus heating them. Thus, neutrons rapidly reach a Maxwellian distribution of speeds and, thus, kinetic energy. In turn, as was alluded to above, these speeds determine how the neutron will interact with a nucleus with which it collides, scattering, absorption, or in the case of heavy nuclei (generally the actinides), fission. The rate and proportion at which these interactions occur will in turn control the population of the neutrons in the fuel.

The rate of change in the population of neutrons, in effect the number of neutrons that will result in fission, determines a parameter in nuclear engineering known as “reactivity,” almost always designated in formulas as k. If k is less than one, the population of neutrons is decreasing, or below a level at which nuclear reactions can be sustained and the fuel is said to be in a subcritical state. If it is exactly one, the population of neutrons is constant, and in a nuclear reactor, this is the state of normal operations, if k is greater than one, the fuel is supercritical, the power output will increase, catastrophically in a nuclear weapon, but in a controlled fashion, during an increase in power level, such as in startup.

The formula for k is known as the "six factor formula" and is nicely described on the linked Wikipedia page devoted to a critical factor in nuclear engineering, excuse the pun.

For convenience, here, reproduced as a graphic from the Wikipedia page is the formula, the meaning of the symbols can be found by clicking on the link, which has an excellent description:



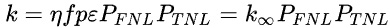
On a macroscopic scale, this effects the physical properties of a fuel, importantly its density, which translates, in turn, to the distance between atoms. In an elementary college level chemistry or physics course, or even such a course in a good high school, one learns that the "size" of atoms is dominated by the probability space of finding electrons, referred to as "orbitals" owing the historically generated planetary model developed by Neils Bohr. The similarity to stellar planetary systems is actually a function of the fact that overall, an atom is largely empty space, at least if one is thinking of an electron as a particle as opposed to thinking of it as a wave function, a distribution of charge. A difference between a planetary model and a stellar system is that in the latter, the star is usually the largest object in the system, whereas in an atom, the nucleus, in terms of "size" is the smallest object.

In the above formula, the factors P_FNL and P_TNL, where the "NL" refers to "non-leakage for respectively fast and thermal neutrons, implies that neutrons leak from the fuel, where they interact with reactor materials, and are lost to the fuel. This loss is effectively a control factor. If neutrons leak from the fuel, they reduce, obviously, the population of neutrons in the fuel. Depending on the nature of the coolant, they may be reflected back into the fuel, absorbed in the coolant depending on the capture cross section of the elements composing the coolant or absorbed in structural reactor components or in control rods or "poisons" added to the coolant.

In the paper under discussion the coolant is liquid sodium metal. This is not the coolant I'd propose in my "crazy idea" of a reactor. Although liquid sodium is the coolant most utilized in fast reactors and represents almost a "default" coolant in the fast neutron spectrum, with LBE (lead bismuth eutectic) in a few reactor types in Russia, other possibilities certainly exist, in fact there are potentially an infinite number of types of coolants. In the paper under discussion, the "coolant temperature coefficient" refers to the fact that the definition of what a "thermal" neutron might be depends on the temperature of the coolant, a fact to which I alluded in the brief above discussion of the Maxwell-Boltzmann distribution law. In liquid sodium, according to the paper, the effect of the coolant temperature coefficient shifts the average speeds of neutrons to a region where the probability of fission is higher, leading to an increase in reactivity, but this can be managed in other cases with different coolants.

Thus in this discussion I will qualitatively address this factor, by saying say the following: In use, nuclear fuel swells, in part from the accumulation of gaseous fission products like xenon and krypton, as well as helium from alpha decay - a factor more important in americium than in plutonium, given the relatively short half lives of ²⁴¹Am and ²⁴³Am compared to the common plutonium isotopes. They are also subject to thermal expansion. Both of these factors increase the distance between atoms, and thus increase the probability that a neutron will pass through the fuel without interacting with an actinide, that is, leak, tending to reduce the population of neutrons in the fuel, stabilizing "k." There is a more subtle point however that is covered in the paper, which is the hardening of the neutron spectrum - increasing the fraction of the neutrons that are "fast" or "epithermal" - which may (and does) affect the probability of neutrons being in a region of a high fission cross section. It is possible to isolate fairly isotopically pure ²⁴¹Am from purified reactor grade plutonium, since it formed from the beta decay of ²⁴¹Pu, which has a half-life of a little over 14 years. Pure ²⁴¹Am would probably be a more problematic fuel than americium consisting of both ²⁴¹Am and ²⁴³Am - the latter can actually dominate the distribution in fuels with long burn up times. One reference I've used in the past (cf: Nuclear Reactor Physics, William E. Stacy, Wiley and Sons 2001. pg.234) claims that in continuously recycled used nuclear fuels, the equilibrium distribution of americium isotopes will be roughly 65% ²⁴¹Am, 5% ^242mAm and 30% ²⁴³Am. ^242mAm is highly fissionable and decays into its nuclear isomer ²⁴²Am, which is also highly fissionable. The case between these two nearly isobaric nuclei is unusual inasmuch as the higher energy isotope,^242mAm, actually has a longer half-life, t_1/2 = 141 years than the lower energy isotope ²⁴²Am, t_1/2 = 16 hours. The latter has a branch ratio so that 82.7% decays into ²⁴²Cm, and 17.3% decays via electron capture into ²⁴²Pu. ²⁴²Pu can absorb a neutron to form short-lived ²⁴³Pu with t_1/2 = 5 hours, decaying to the ²⁴³Am. ²⁴³Am serves a role much like that of ²³⁸U in traditional nuclear fuels. It absorbs a neutron without fission, thus reducing the population of neutrons for at least the short term, decaying via an intermediate ²³⁹Np to ²³⁹Pu fissionable plutonium. This process is relatively slow, since the for ²³⁹Np, t_1/2 = 2.4 days, slowing the rise of reactivity making it easier to control. This is not the case for ²⁴¹Am where absorption of a neutron leads directly to a highly fissionable fuel, one of the two 242 isotopes. Thus it is desirable, to control the neutron population, to have ²⁴³Am in the fuel, to absorb neutrons to produce ²⁴⁴Am, t_1/2 = 10.1 hours to give fairly inert (with respect to fission) ²⁴⁴Cm, which is useful as a heat source in thermoelectric devices such as those used on space craft, with a higher energy output than commonly used ²³⁸Pu, albeit with a shorter half-life.

This leaves the third point, the smaller delayed neutron factor.

There are two kinds of neutron releases in a nuclear reactor, "prompt neutrons" which appear immediately on fission, and "delayed neutrons" which come from an unusual decay mode of fission products, neutron emission. For neutron emission to occur the fission product has to be very neutron rich. In traditional uranium fueled nuclear reactors, significant components of the light fraction of fission products, notably heavy isotopes of bromine, contribute delayed neutrons. Delayed neutrons are considered important since they add an element of time to allow the insertion of control rods in traditional types of nuclear reactors to lower the neutron flux and eliminate criticality.

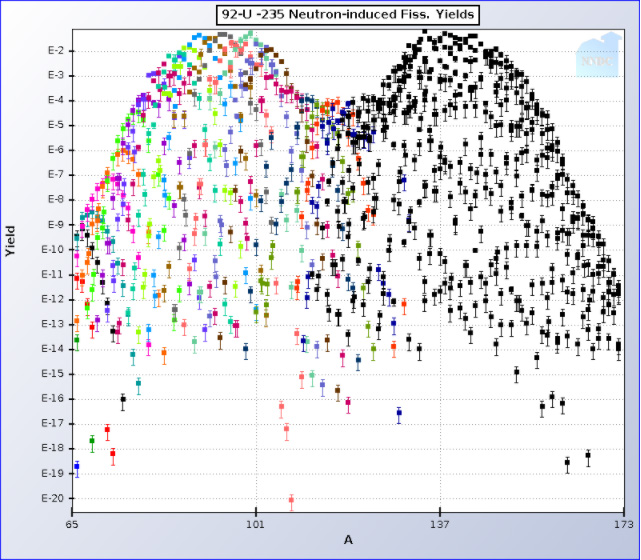
Nuclear fission as asymmetric with respect to the distribution of mass numbers of the fission products. Graphically, for most of the mid range actinides that dominate nuclear fuels today, uranium and plutonium, this distribution looks like camel humps. Here for instance is a plot of the fission products of ²³⁵U, the main fissionable isotope in the commercial nuclear fleet, which uses "enriched" uranium:



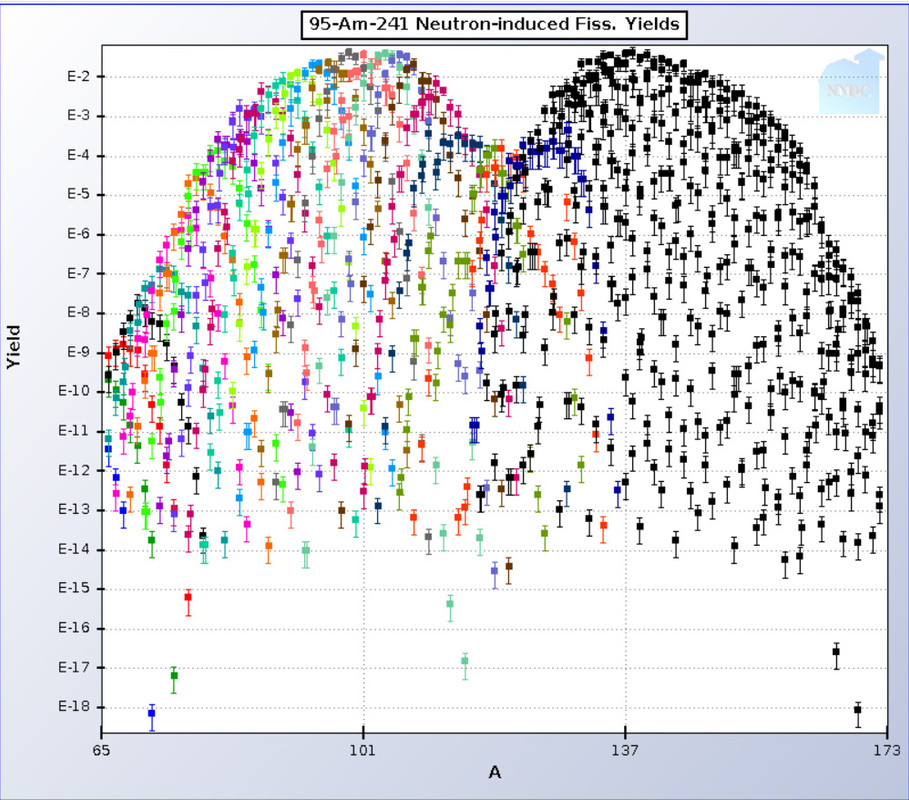
Here is the same distribution map for ²⁴¹Am:



Note in the first case, the hump on the left is centered at a mass number of around 90, which corresponds to the major valuable fission product ⁹⁰Sr, which has been used in portable thermoelectric devices for power supplies in remote systems since the heat output is about half a watt per gram as it decays to stable ⁹⁰Zr via the short-lived intermediate ⁹⁰Y.
(In the former Soviet Union, these power supplies were used near the arctic coast for lighting.)

In the case of ²⁴¹Am, however the left hump is centered around mass number 100, which corresponds to the stable isotope of the valuable element ruthenium, an important industrial catalyst material. (The world supply of the extremely rare and valuable nearby monoisotopic element rhodium, with a mass number of 103 is greater in used nuclear fuels than it is in economically recoverable ores.)

In general, as the mass of actinides undergoing fission increases, the right hump doesn't move much - it accounts for the presence of the light lanthanides in used nuclear fuel, whereas the left hump moves to the right, until they coalesce in isotopes of fermium, which will never be available in visible amounts owing to its very short half life.

The paper cited at the outset of this post shows this effect more clearly than the distributions shown immediately above, by focusing solely on fission product mass numbers, in this case comparing the fission product profile of ²³⁵U with that of the fissionable nuclide ²⁴⁵Cm on the same graph:



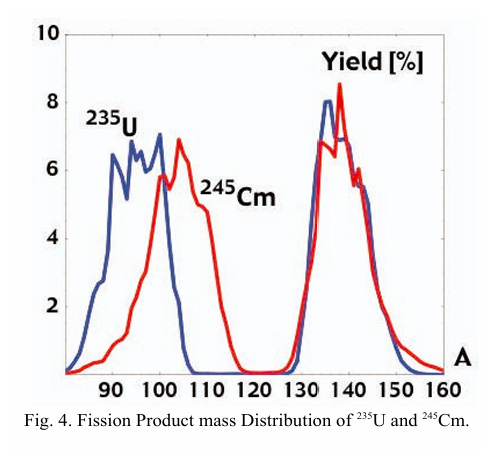
In terms of delayed neutrons, this disparity in yields results in the absence of several important sources of delayed neutrons present in ²³⁵U, specifically certain heavy short lived isotopes of bromine with mass numbers in the low 90s and rubidium in the high 80s. Other sources of delayed neutrons, such as heavy isotopes of iodine and cesium (not mentioned in the paper) are unchanged.

I cannot go into the details here - this post is already rather long - but the safety point of avoiding transients, known as "UTOP," "Unprotected Transient Over power" would be an issue in a traditional rod based nuclear fuel, which is the type of fuel discussed in the paper. To prevent this I'd propose a passive control system based on the biphasic coolant to which I alluded above. The issue is addressable to my mind. An additional safety parameter would be to allow partial deliberate melting of a metallic americium fuel in a coolant with a higher boiling point than the melting point of americium, 1443K, so as to render it briefly subcritical. The reactor would be designed to be operationally unaffected in this case, and subject to continuing operation simply by adding more americium fuel to the system to replace that lost by melting.

An important feature of the reactor design I envision is operation at very high temperatures, well above the critical temperature of water, so as to allow for process intensification to use nuclear heat to produce things more valuable than electricity, with electricity being a side product. The heat transfer aspects are very much tied to boiling metals and boiling salts of a particular design. Almost the entire reactor is made from the components of used nuclear fuels.

This system would be neutron rich, and as I envision it, it would feature a depleted uranium blanket, nearly pure ²³⁸U, transmuting it into ²³⁹Pu, to allow for a safe and sustainable world. We need to access fissionable nuclei as fast as is possible if we are to have any hope of saving what is left to be saved, and possibly even restore some of what has been lost but remains subject to restoration.

This is a long post, and not particularly sophisticated for advanced nuclear engineers, since there's admittedly a bit of "handwaving" but I think as crazy ideas go, I believe it might have some merit that might inspire some level of thinking more sophisticated engineers, with real access to valuable used nuclear fuels containing americium. I wrote it to reify some of the ideas that float around in my head from time to time. I trust that the reader who got this far is not annoyed by it.

Have a pleasant Sunday.