Newly discovered 'einstein' tile is a 13-sided shape that solves a decades-old math problem

[Judi Lynn]

By Paul Sutter published about 3 hours ago

A new 13-sided shape is the first example of an elusive "einstein" — a single shape that can be tiled infinitely without repeating a pattern.



This computer-generated image shows a newfound shape arranged in concentric rings around a central, shaded "hat" (dark blue). (Image credit: Smith et al. (2023))


Look carefully! Mathematicians have invented a new 13-sided shape that can be tiled infinitely without ever repeating a pattern. They call it "the einstein."

For decades, mathematicians wondered if it was possible to find a single special shape that could perfectly tile a surface, without leaving any gaps or causing any overlaps, with the pattern never repeating. Of course, this is trivial to do with a pattern that repeats — just look at a bathroom or kitchen floor, which is probably made up of simple rectangular tiles. If you were to pick up your floor and move it (called a "translation" in mathematics), you could find a position where the floor looks exactly the same as before, proving that it's a repeating pattern.

In 1961, mathematician Hao Wang conjectured that aperiodic tilings, or tilings that never become a repeating pattern, were impossible. But his own student, Robert Berger, outwitted him, finding a set of 20,426 shapes that, when carefully arranged, never repeated. He then slimmed that down to a set of 104 tiles. That means that if you were to buy a set of those tiles, you could arrange them on your kitchen floor and never find a repeating pattern.

In the 1970s, Nobel prize-winning physicist Roger Penrose found a set of only two tiles that could be arranged together in a nonrepeating pattern, now known as a Penrose tiling.



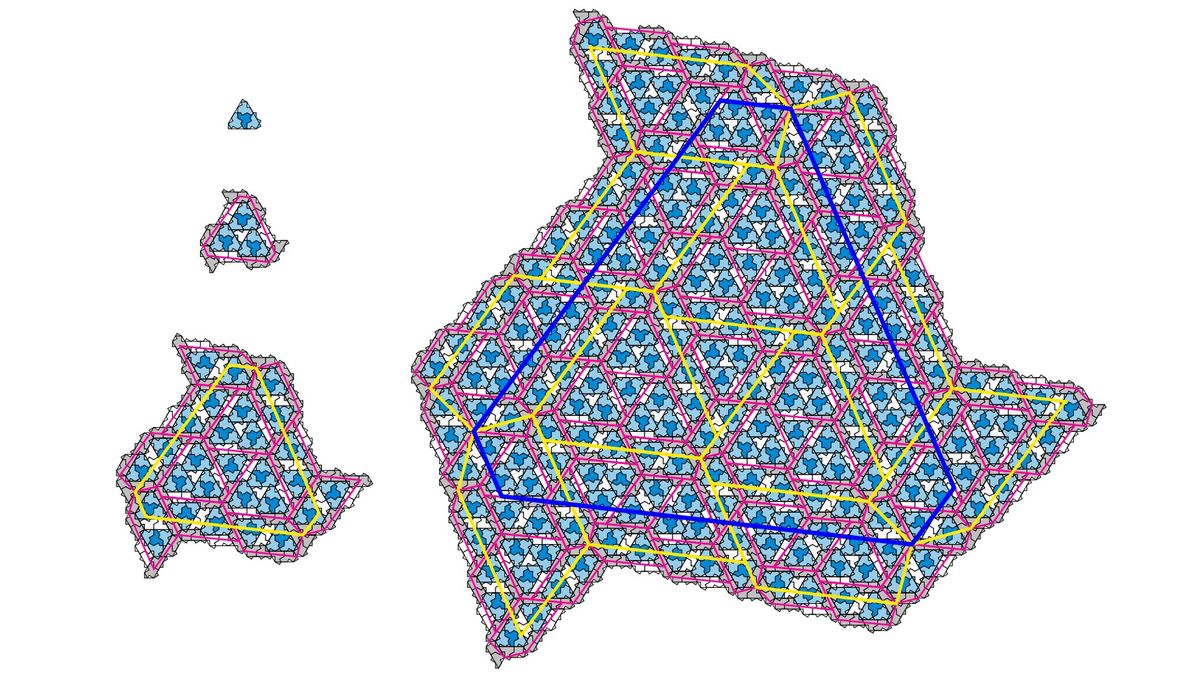
Here we see the first four iterations of the H metatile and its supertiles. (Image credit: Smith el at. (2023))

More:
https://www.livescience.com/newly-discovered-einstein-tile-is-a-13-sided-shape-that-solves-a-decades-old-math-problem

[cos dem]

1. This is awesome. Thanks for posting

I always wanted to tile something with Penrose tiles.
Now I’ll have to change my plans, lol!